在实验室中,样本可以做出质控图
2018-08-30
作者:
浏览数:2389
国家标准GB/T 28863-2012《商品质量监督抽样检验程序具有先验质量信息的情形》对质量特性值标准差的计算给出了一种“均值图与标准差图”计算方法, 但在某些情形下, 取得合理的子组或者不可能或者不实际, 如由于测量单个观测值所需要的时间太长或费用太大, 导致不能考虑重复测量时;如测量很昂贵 (例如破坏性试验) 或者任一时刻的输出都相对均匀时。本文将介绍一种单值控制图的方法, 用较少的测量值计算质量特性值标准差, 提升应用的便利性。
1 单值控制图方法解析
如果不能取得合理子组 (如测量单个测量值所需时间太长或者费用太大) , 或测量昂贵 (如破坏性试验) , 或只有一个可能的数值 (如仪表读数) 等, 则选择至少6个有代表性的生产企业, 每个生产企业收集10个以上测量值。用于数据收集的产品应是同一企业同一原料同一工艺生产的同一批次或连续批次。分别计算出各企业的质量特性值标准差, 取平均值作为该质量监督质量特性值标准差。计算步骤如下:
计算某个生产企业的质量特性标准差s估计值。
(1) 计算平均值。
(2) 计算另两个相邻值的差值的绝对值R (移动极差) , 再计算得出极差的平均值。
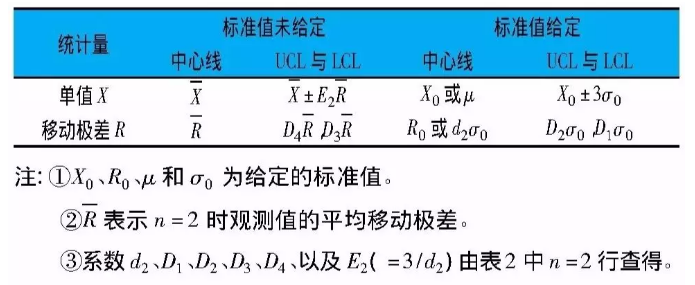
(3) 根据GB/T 4091-2001《常规控制图》, 由表1和表2得出移动极差控制图和单值控制图。
表1 单值控制图的控制限公式
(4) 计算过程能力指数 (PCI)

式中:UTL—上容差限;
LTL—下容差限;

表2 计量控制图计量控制线的系数表

资料来源:ASTM, Philadelphia, PA.USA.
(5) 若有测量值落在移动极差控制图和单值控制图的控制线外, 应剔除, 并重新计算, 直到移动极差控制图和单值控制图都没有异常, 且过程能力指数 (PCI) ≥1, 可算出标准差s估计值。
(6) 以此类推, 可分别得到其他生产企业的标准差估计值。
(7) 取所有企业标准差的平均值作为质量监督中的标准差。
2 应用示例
某商品质量监督机构为了确定奶粉水分的标准差值, 选择了6个有代表性的生产企业, 收集了关于奶粉水分的生产控制数据, 见表3。
表3 A公司连续10个奶粉样品的水分含量百分比
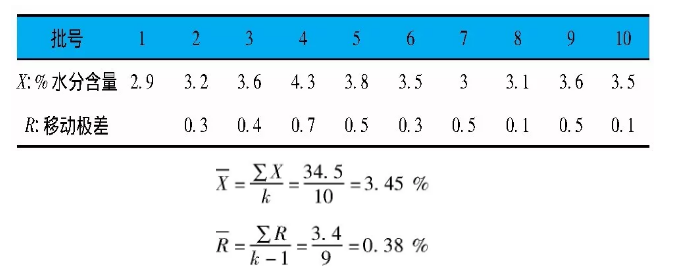
第一步, 绘制移动极差 (R) 控制图并评估控制状态, 中心线
系数D3和D4的值由表2中按n=2行查得, 由于表3中的R值都位于R图的控制限内, 故R图显示出过程处于统计控制状态。因此,值可用来计算X图的控制限。
图1
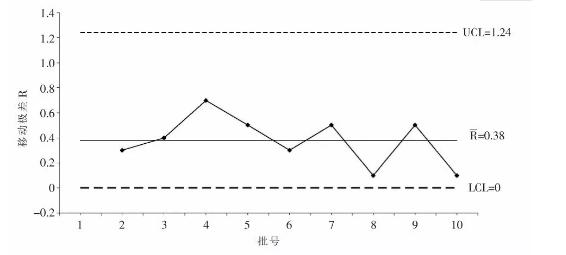
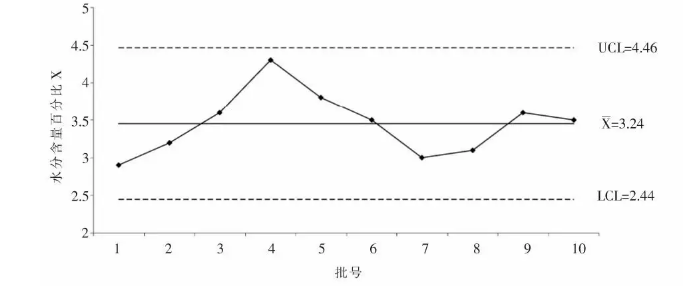
第二步, 绘制单值 (X) 控制图并评估控制状态中心线
系数E2的值由表1和表2给出。由于表3中的X值都位于X图的控制限内, 故X图显示出过程处于统计控制状态。
图2
当PCI>1时, 过程能力指数可认为是足够的。则A公司生产的奶粉水分的标准差为0.4197。
以此类推, 可分别得到6个公司生产的奶粉水分的标准差, 取这些标准差的平均值作为质量监督中的标准差。








